Chord Progressions
diatonic / scale-tone chords
Quite simply, chord progressions are a series of chords that sound good together. They originate from the root chord and are the foundation of popular music styles throughout the Western world.
Their function is to establish the key of a song or piece of music, and are expressed using the name and type of each chord.
For Example: In the Key of C Major the 'C' indicates the root note, and the 'Major' indicates the type of chord. In the key of A Minor, the 'A' indicates the root note, and the 'Minor' - the type of chord.
Progressions are commonly expressed as Roman Numerals using uppercase for major chords and lowercase for minor chords with an added superscript ° for a diminished chord (I–ii-iii-IV-V-vi-vii°).
Every major and minor key comes with its own set of seven diatonic chords (3 major/3 minor/1 diminished).
Diatonic = belonging to, or derived from, the notes of a particular scale.What chords can I play?
It's important to know what chords can be played in a progression. This depends on the key you are in. Once you determine the key, e.g. C Major
- write down the scale: C - D - E - F - G - A - B (no sharps or flats)
- formula for a major scale: I–ii-iii-IV-V-vi-vii° (uppercase/major - lowercase/minor)
- combine each note of the scale into the formula: C - Dm - Em - F - G - Am - B° (See Table 1 for all major and minor keys.)
In the key of C Major, you can use any of these chords in your progression, but which of these chords sound good together when played in succession? Let's take a look at some popular progressions.
Two-Chord Progressions
- I - V : The most basic progression alternates between 2 chords. This occurs between the 1st (tonic) and 5th(dominant) degree of a scale. They are repeated over and over e.g., C - G - C - G - C.
A good example of this is Achy Breaky Heart by Billy Ray Cyrus in the key of A major with chords, A and E. - I - IV : Another basic progression is played between the 1st (tonic) and 4th (sub-dominant) degrees of a scale e.g., A - D - A - D - A
Three-Chord Progression using Primary Chords
The most popular 3-chord progressions are based on the first, fourth, and fifth degrees of a diatonic scale: I - IV - V. These are called Primary Chords - doesn't matter if you are in a Major or Minor key:
- Primary chords are major chords in a Major Key
- Primary chords are minor chords in a Minor Key
We will illustrate this using the key of C Major and its relative key of Am - they both share the same key signature of no sharps or flats.
- In the key of C major, the primary chords are major chords: C - F - G
- In the key of Am, the primary chords are minor chords: Am - Dm - Em
The I - IV - V (1 - 4 - 5) progression can be used in a number of ways. Let's look at some examples:
- I - IV - V - V... La Bamba by Richie Valens
- I - I - IV - V... Get Off Of My Cloud by The Rolling Stones
- I - IV - I - V... The Lion Sleeps Tonight by The Tokens
- I - IV - V - IV...Wild Thing by The Troggs
12 Bar Blues uses a longer form of the I - IV - V progression utilizing 12 bars, hence its name. There are many variations, but the most common and popular chord progression which is significant in the rock 'n' roll genre is:
I - I - I- I - IV - IV - I - I - V - V- I - I
So if you were playing 12 bar blues in the key of E, it would go like this:
E - E - E - E - A - A - E - E - B - B - E - E
ORE - E - E - E - A - A - E - E - B - A - E - E
Secondary Chords
Secondary Chords are based on the second, third, sixth and seventh degrees of a diatonic scale:II - III - VI - VII
- In C Major secondary chords are: Dm - Em - Am - Bdim
- In Am secondary chords are: Bdim - C - F - G
A diminished or dim chord is a minor chord with a flattened fifth: 1 - b3 - b5
Common Progression using Primary & Secondary Chords:
I – V – vi – IV progression is used in several music styles. In C Major the progression would be:
C - G - Am - F.
These chords can be played in a variety of ways depending on the mood you are trying to create: Remember, lower-case letters represent minor chords.
- I – V – vi – IV : C–G–Am–F
- V – vi – IV – I : G–Am–F–C
- vi – IV – I – V : Am–F–C–G
- IV – I – V – vi : F–C–G–Am
Circle progressions
A great way to move through all primary and secondary chords in a diatonic scale is to use the circle of fifths - an extremely useful tool in music composition. It shows all 12 tones of the chromatic scale along with the relationships between major and relative minor key signatures - very handy for chord progressions in any given key... also great for key signatures.
Circle Progressions utilize the Circle Of Fifths whereby adjacent root notes have an ascending - descending relationship.
If you move counterclockwise around the circle there is a repeated chord movement of 'up a 4th - down a 5th' etc.
This method uses all 7 chords in a Diatonic Scale and is the most common and the strongest of all harmonic progressions.
The result: I–IV–vii°–iii–vi–ii–V–I (Start and finish on the tonic or root note)
If you move clockwise around the circle there is a repeated chord movement of 'up a 5th - down a 4th' etc.
The result: I–V–ii–vi–iii–vii°–IV–I (Start and finish on the tonic or root note)
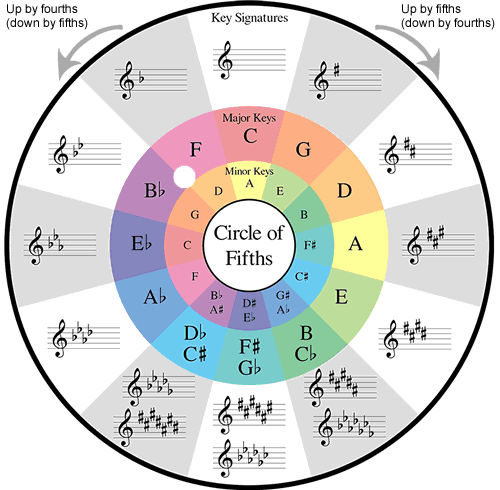
Let's take a look at how we get there
| C Major Scale (no sharps or flats) | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| Scale Degrees | I | ii | iii | IV | V | vi | vii° |
| Circle Of Fifths - Counterclockwise | C | F | B | E | A | D | G |
| Chord Progression | I | IV | vii° | iii | vi | ii | V |
| Chord & Type | C | F | B° | Em | Am | Dm | G |
| Circle Of Fifths - Clockwise | C | G | D | A | E | B | F |
| Chord Progression | I | V | ii | vi | iii | vii° | IV |
| Chord & Type | C | G | Dm | Am | Em | B° | F |
Usable Chords In Every Key
In every key, there is a progression of chords which establishes a foundation of triads on which chord progressions are built.
In each key you will find all the usable chords which can be used in a number of ways - determining chords and keys to a particular song, composing, song writing etc.
Table 1:| Major Key | I | ii | iii | IV | V | vi | viiº |
|---|---|---|---|---|---|---|---|
| C | C | Dm | Em | F | G | Am | Bº |
| G | G | Am | Bm | C | D | Em | F#º |
| D | D | Em | F#m | G | A | Bm | C#º |
| A | A | Bm | C#m | D | E | F#m | G#º |
| E | E | F#m | G#m | A | B | C#m | D#º |
| B | B | C#m | D#m | E | F# | G#m | A#º |
| F# | F# | G#m | A#m | B | C# | D#m | E#º |
| C# | C# | D#m | E#m | F# | G# | A#m | B#º |
| F | F | Gm | Am | B♭ | C | Dm | Eº |
| B♭ | B♭ | Cm | Dm | E♭ | F | Gm | Aº |
| E♭ | E♭ | Fm | Gm | A♭ | B♭ | Cm | Dº |
| A♭ | A♭ | B♭m | Cm | D♭ | E♭ | Fm | Gº |
| D♭ | D♭ | E♭m | Fm | G♭ | A♭ | B♭m | Cº |
| G♭ | G♭ | A♭m | B♭m | C♭ | D♭ | E♭m | Fº |
| C♭ | C♭ | D♭m | E♭m | F♭ | G♭ | A♭m | B♭º |
| Minor Key | i | iiº | III | iv | v | VI | VII |
|---|---|---|---|---|---|---|---|
| Am | Am | Bº | C | Dm | Em | F | G |
| Em | Em | F#º | G | Am | Bm | C | D |
| Bm | Bm | C#º | D | Em | F#m | G | A |
| F#m | F#m | G#º | A | Bm | C#m | D | E |
| C#m | C#m | D#º | E | F#m | G#m | A | B |
| G#m | G#m | A#º | B | C#m | D#m | E | F# |
| D#m | D#m | E#º | F# | G#m | A#m | B | C# |
| A#m | A#m | B#º | C# | D#m | E#m | F# | G# |
| Dm | Dm | Eº | F | Gm | Am | B♭ | C |
| Gm | Gm | Aº | B♭ | Cm | Dm | E♭ | F |
| Cm | Cm | Dº | E♭ | Fm | Gm | A♭ | B♭ |
| Fm | Fm | Gº | A♭ | B♭m | Cm | D♭ | E♭ |
| B♭m | B♭m | Cº | D♭ | E♭m | Fm | G♭ | A♭ |
| E♭m | E♭m | Fº | G♭ | A♭m | B♭m | C♭ | D♭ |
| A♭m | A♭m | B♭º | C♭ | D♭m | E♭m | F♭ | G♭ |
How do we make our progressions more interesting?
Now for the exciting part! We will show you how to build on your chord progressions with chord extensions adding interest to many progressions using Scale Tone Chords.
By adding thirds we will go from triads all the way to 13th chords, giving you a wide variety of chords to choose from.
Scale Tone Chords and Stacking Thirds
Every key has its own set of chords that can be constructed using the notes of that key. These are called Diatonic Chords or Scale Tone Chords.
The term Scale Tone Chords is used here because it helps beginners understand that these chords are derived from the notes, or tones, of the given scale.
Each chord is constructed by the combination of notes which are a third apart — in a typical 3-note chord or triad, we have:
We will use the C Major Scale as an example: C - D - E - F - G - A - B where each third interval will be written in Roman Numerals as follows, I - II - III - IV - V - VI - VII.
Using the C Major Scale, we can construct scale tone chords by stacking 2 consecutive third intervals above each note.
| C Major Scale | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| III (+ a diatonic 3rd) | E | F | G | A | B | C | D |
| V (+ a diatonic 3rd) | G | A | B | C | D | E | F |
| Constructed Chord | C | Dm | Em | F | G | Am | Bº |
Even though each chord name is derived from its root note, they are all C scale tone chords because they only contain notes from the C Major Scale - no sharps or flats.
This can be done for each major scale, giving us a group of chords that can be derived from any key, by simply stacking 3rd intervals on each root scale note.
Let's look at another example: F Major Scale which consists of 1 flat - B♭
| F Major Scale | F | G | A | B♭ | C | D | E |
|---|---|---|---|---|---|---|---|
| III (+ a diatonic 3rd) | A | B♭ | C | D | E | F | G |
| V (+ a diatonic 3rd) | C | D | E | F | G | A | B♭ |
| Constructed Chord | F | Gm | Am | B♭ | C | Dm | Eº |
They are all F scale tone chords because they only contain notes from the F Major Scale - 1 flat - B♭.
Scale Tone Chord Extensions...
What happens if we add another third to our existing triad or 3 note chord from the C Major Scale:
Table 4:
| C Major Scale | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| III (+ a diatonic 3rd) | E | F | G | A | B | C | D |
| V (+ a diatonic 3rd) | G | A | B | C | D | E | F |
| VII (+ a diatonic 3rd) | B | C | D | E | F | G | A |
| Constructed Chord | Cmaj7 | Dm7 | Em7 | Fmaj7 | G7 | Am7 | Bø7 |
Let's use the earlier circle progression: I–IV–vii°–iii–vi–ii–V–I in C Major and include diatonic 7ths:
- Triads Only: C - F - B° - Em - Am - Dm- G - C
- Including 7ths: Cmaj7 - Fmaj7 - Bø7 - Em7 - Am7 - Dm7 - G7 - Cmaj7... very nice!
We can now add more chords to our progressions. 7th Scale tone chords for all keys:
| Scale Degree | I | ii | iii | IV | V | vi | viiº |
|---|---|---|---|---|---|---|---|
| Chords | maj7 | m7 | m7 | maj7 | dom 7 | m7 | ø7 |
Add more chords to your standard chord progressions...
You can keep adding thirds in the same fashion, and build 9th (octave above sus2), 11th (octave above sus4), and 13th (octave above a 6th) chord. If we continue to use the C Major Scale as an example, we derive the following:
| C Major Scale | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| III (+ a diatonic 3rd) | E | F | G | A | B | C | D |
| V (+ a diatonic 3rd) | G | A | B | C | D | E | F |
| Constructed Chord | C | Dm | Em | F | G | Am | Bº |
| VII (+ a diatonic 3rd) | B | C | D | E | F | G | A |
| Constructed Chord | Cmaj7 | Dm7 | Em7 | Fmaj7 | G7 | Am7 | Bø7 |
| IX (+ a diatonic 3rd) | D | E | F | G | A | B | C |
| Constructed Chord | Cmaj9 | Dm9 | Em9 | Fmaj9 | G9 | Am9 | Bø9 |
| XI (+ a diatonic 3rd) | F | G | A | B | C | D | E |
| Constructed Chord | Cmaj11 | Dm11 | Em11 | Fmaj11 | G11 | Am11 | Bø11 |
| XIII (+ a diatonic 3rd) | A | B | C | D | E | F | G |
| Constructed Chord | Cmaj13 | Dm13 | Em13 | Fmaj13 | G13 | Am13 | Bø13 |
Notice that all the notes used to construct these chords come from the C Major scale. These are therefore diatonic chords of C Major, also referred to here as C Major Scale Tone Chords.
Note: Extended chords such as Fmaj13 contain more chord tones than can be played simultaneously on a 6-string guitar, so practical guitar voicings may omit one or more notes.
Chord Extensions & Related Chords:
- The 9th is the same scale degree as the 2nd, but one octave higher. This means we can also use sus2 chords in our progressions. For example, Csus2, Fsus2 and Gsus2 can all be constructed using notes from the C Major scale, with no sharps or flats.
- The 11th is the same scale degree as the 4th, but one octave higher. This means we can also use sus4 chords in our progressions. For example, Csus4 and Gsus4 can all be constructed using notes from the C Major scale, with no sharps or flats.
- The 13th is the same scale degree as the 6th, but one octave higher. This means we can also use 6 chords in our progressions. For example, C6, F6 and G6 can all be constructed using notes from the C Major scale, with no sharps or flats.
In Summary: Scale Tone Chords for C Major
Starting with the seven diatonic triads of C Major, we can create many additional chords using only the notes of the C Major scale.
Table 7:| Standard Chord Progression: C - Dm - Em - F - G - Am - Bdim | |
|---|---|
| Additional C chords | Csus2 / Csus4 / C6 / Cmaj7 / Cmaj9 / Cmaj11 / C maj13 |
| Additional Dm chords | Dm6 / Dm7 / Dm9 / Dm11 / Dm13 |
| Additional Em chords | Em7 / Em9 / Em11 / Em13 |
| Additional F chords | Fsus2 / F6 / Fmaj7 / Fmaj9 / Fmaj11 / Fmaj13 |
| Additional G chords | Gsus2 / Gsus4 / G6 / G7 / G7sus4 / G9 / G11 / G13 |
| Additional Am chords | Am7 / Am9 / Am11 / Am13 |
| Additional B dim chord | Bø7 / Bø9 / Bø11 / Bø13 |
This table shows common additional chords that can be derived from the notes of a major scale for each of the seven diatonic chord degrees.
Table 8:| I | ii | iii | IV | V | vi | viiº |
|---|---|---|---|---|---|---|
| sus2 | m6 | m7 | sus2 | sus2 | m7 | ø7 |
| sus4 | m7 | m11 | 6 | sus4 | m9 | ø9 |
| 6 | m11 | m13 | maj7 | 6 | m11 | ø11 |
| maj7 | m13 | maj9 | 7 | m13 | ø13 | |
| maj9 | maj11 | 7sus4 | ||||
| maj13 | maj13 | 9, 11, 13 |
Relationship between Major and Minor Scales
Each major scale has a relative minor scale that shares exactly the same notes, e.g., the relative minor of C Major is A Minor. The natural minor scale is the sixth mode of the major scale - if you look at the 6th degree of a C major Scale you will reach A — see table 1 where all major scales are listed followed by their relative minor scales in the same order.
Notice that Am and C major scales have no sharps or flats and have exactly the same chords except that the first note for the minor scale is A and the first constructed chord is Am.
The constructed chords in the table are all triads (3-note chords). If you find yourself using a minor key, the chords will be exactly the same as its relative major key starting on the 6th degree of the scale.
P.S. If you are using a Bm Scale, you can use the same chords as a D Major Scale (starting on the 6th degree of the D major scale)— the chords are exactly the same.
Alternatively, if you are in a major or minor scale and want to determine it's relative Scale:- Major Scales are 3 semitones up from a Minor Scale's Root Note: (e.g., Em → G):
- E Minor Scale: E F♯ G A B C D E
- Relative Major of E Minor: Three semitones up from E is G, so the relative major scale of E Minor is G Major (G major scale: G A B C D E F♯ G).
- They share the same notes
- Minor Scales are 3 semitones down from a Major Scale's Root Note (e.g., G → Em):
- G Major Scale: G A B C D E F♯ G
- Relative Minor of G Major: Three semitones down from G is E, so the relative minor scale of G Major is E Minor (E natural minor scale: E F♯ G A B C D E).
- They share the same notes
Learn to listen
A good ear will be able to choose the chords that sound 'right' in a given piece of music. Even a 'not so good ear' can often tell if a chord is not right... consider the following:
A little story I like to tell:When I was performing, my manager would often come to my gigs. She considered herself to be tone-deaf, but if I ever hit a wrong note or chord, she would always turn around and give me that 'you hit a wrong note' look... she knew. She wasn't a musician and couldn't sing or pitch in the right key, but she knew when a note or chord wasn't right because it didn't sound right. So, if you are a musician, you will most likely know if a note or chord doesn't sound right.
I hope you have enjoyed this session. Next time you are writing a song and you want to know what chords are available for you to play in a particular key, use 'the chart' ... very handy.
Then you may want to spice things up a bit with some extended chords. Play around with some of your own chord progressions - you may surprise yourself. If it sounds good, that's the progression for you!
Top Pick: Guitar Cheat Sheets at Amazon
A practical guitar reference chart pack featuring chord, scale, triad and circle of fifths cheat sheets to help players understand key music theory concepts.
