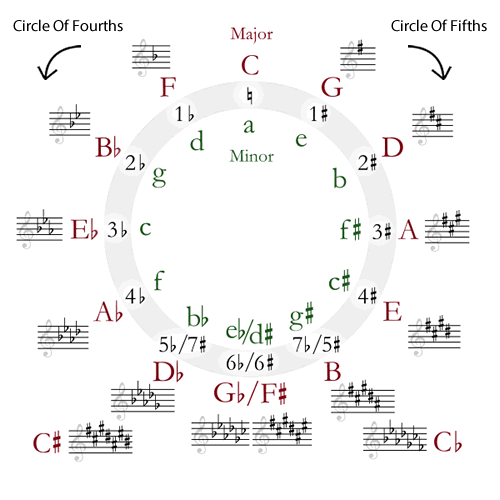
Circle of Fifths

Mastering the Circle of Fifths:

The Circle of Fifths is an invaluable tool for beginners learning music theory, especially when trying to understand key relationships, chord progressions, and scales. Here are some practical uses for beginners:

• How to Use: The Circle of Fifths helps identify the key signature for major and minor keys. Starting at the top with C Major (no sharps or flats), each step clockwise adds one sharp, while each step counterclockwise adds one flat.
• Practical Application: If you're learning a song in G Major, the circle tells you that G Major has one sharp (F#). Similarly, if a song is in F Major, you'll see it has one flat (Bb).
• Tip: Beginners can use this to quickly identify the accidentals (sharps or flats) in any key.

• How to Use: Common chord progressions are based on relationships between the tonic (I), dominant (V), and subdominant (IV) chords. These chords are adjacent to each other on the Circle of Fifths.
• Practical Application: In the key of C Major, the chords C (I), G (V), and F (IV) are close together on the circle, making them easy to spot for building basic progressions. For a song in G Major, you'd use G (I), D (V), and C (IV).
• Tip: This helps with quick composition or recognizing common progressions like I-IV-V in any key.

• How to Use: Every major key has a relative minor, which shares the same key signature. On the Circle of Fifths, the relative minor is located just inside the outer circle of major keys.
• Practical Application: If you're playing in C Major but want to switch to its relative minor (A minor), the Circle shows that they share the same notes, helping you switch smoothly.
• Tip: This is useful for composing or improvising within the same key signature but giving a different tonal feel.

• How to Use: The Circle of Fifths can be used to transpose songs from one key to another by moving the same number of steps around the circle.
• Practical Application: If a song is too high to sing in E Major, you can use the Circle of Fifths to easily transpose it down to D Major by moving counterclockwise.
• Tip: Beginners can use the Circle to maintain the same chord relationships while changing keys for more comfortable playing or singing.

• How to Use: The Circle of Fifths helps visualize the relationship between scales. Moving clockwise from C Major, the scales gain one sharp; moving counterclockwise, they gain one flat.
• Practical Application: If you're learning scales, you can use the Circle to figure out which notes are sharp or flat in each key. For example, if you're learning the G Major scale, you know it will have F# based on the circle.

• How to Use: The Circle of Fifths shows which keys sound good together for modulation (changing keys within a song).
• Practical Application: If you want to add variation to a song in C Major, you can easily modulate to G Major (one step clockwise) or F Major (one step counterclockwise) for smooth transitions.
• Tip: This helps create interesting and dynamic songs while maintaining a smooth, cohesive sound.

• How to Use: The Circle of Fifths can help identify common chord substitutions. Chords that are close to each other on the circle can often substitute for one another.
• Practical Application: In a song in the key of C, instead of playing G major (V), you could substitute it with a D minor (ii) to add harmonic interest.
• Tip: This is helpful for adding creativity to chord progressions without breaking music theory rules.

• How to Use: The Circle helps beginners visualize strong cadences (musical phrases). The V-I cadence (dominant to tonic) is a fundamental resolution.
• Practical Application: In the key of C Major, G (V) resolves naturally to C (I). The circle makes this relationship clear and shows you how to find these cadences in other keys.
• Tip: Practicing cadences in various keys can improve your musical phrasing and understanding of resolution.

The Circle of Fifths can be an incredible resource for beginners as it visually organizes musical concepts and relationships, making them easier to understand and apply... it doesn't get much better than that.

Common Musical Intervals

To provide a quick reference, here are some common musical intervals and their corresponding half steps or semitones:

• Perfect Unison: 0 half steps (the same note)
• Minor Second: 1 half step
• Major Second: 2 half steps
• Minor Third: 3 half steps
• Major Third: 4 half steps
• Perfect Fourth: 5 half steps
• Augmented Fourth (or Tritone): 6 half steps
• Perfect Fifth: 7 half steps
• Minor Sixth: 8 half steps
• Major Sixth: 9 half steps
• Minor Seventh: 10 half steps
• Major Seventh: 11 half steps
• Perfect Octave: 12 half steps

Counterclockwise - Perfect Fourths

Moving clockwise around the Circle of Fifths adds a perfect fifth (7 semitones) to each interval, which takes you to the next key with one more sharp.

Moving counterclockwise adds a perfect fourth (5 semitones) to each interval, which takes you to the next key with one more flat.

• From C major, moving counterclockwise brings you to F major, which has one flat (Bb). The notes in the F major scale are F, G, A, Bb, C, D, E..
• From F major, moving counterclockwise brings you to Bb major, which has two flats (Bb, Eb). The notes in the Bb major scale are Bb, C, D, Eb, F, G, A.

The reason counterclockwise on the Circle of Fifths creates perfect fourths is because of the inverse relationship between a perfect fifth and a perfect fourth: they complement each other to complete an octave (12 half-steps).

A perfect fifth spans 7 semitones, and a perfect fourth spans 5 semitones, adding up to 12 semitones, which is one octave.